[Theory] Tree

09 Mar 2022

트리(Tree)

가게도와 같은 계층적인 구조를 표현할 때 사용 할 수 있는 자료구조입니다.

가장 맨 상위에 뿌리(Root)에서 부터 가지를 치며 빠져나가는 구조로 볼 수 있다.

트리의 관련용어

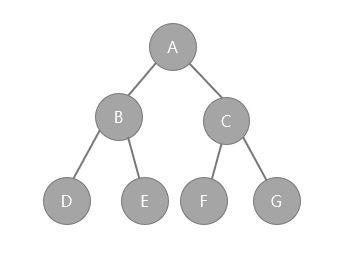
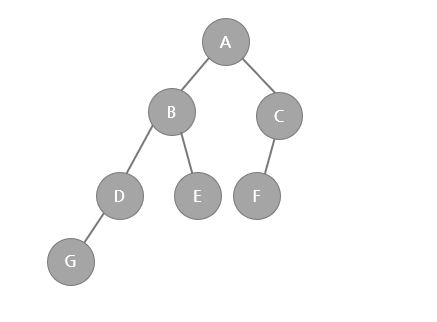
위의 그림을 토대로 트리의 용어와 연결지어 보자.

• 루트 노드 (root node) : 부모가 없는 최상위 노드이며, A노드가 해당된다.
• 단말 노드 (leaf node) : 자식이 없는 노드를 말한다. F, E, G 노드가 해당된다.
• 비 단말 노드(branch node) : 자식 노드를 하나 이상 가진 노드를 말한다. A, B, C, D 노드가 해당된다.
• 부모 노드 (parent node) : 자식 노드를 가진 노드이며, B의 부모 노드는 A이다.
• 자식 노드 (child node) : 부모 노드의 하위 노드를 말하며, A의 자식 노드에는 B, C가 있다.
• 형제 노드 (Sibling node) : 같은 부모를 가지는 노드를 말한다. D, E는 같은 부모 노드인 B를 가진 형제 노드이다.
• 크기 (size) : 트리에 포함된 모든 노드의 갯수. 해당 트리의 크기는 7이다.
• 깊이 (depth) : 루트 노드부터의 거리를 말한다. 각 노드의 깊이는 다음과 같이 볼 수 있다.
  • A 노드 : 0
  • B, C노드 : 1
  • D, E, F 노드 : 2
  • G 노드 : 3
• 높이 (height) : 깊이 중 최댓값, G번 노드인 3을 높이라고 볼 수 있다.
• 차수 (degree) : 각 노드의 (자식 방향) 간선 갯수이며 각 노드의 차수는 다음과 같습니다.
  • A, B 노드 : 2
  • C, D 노드 : 1
  • E, F, G 노드 : 0

트리의 특징

• 트리는 그래프의 한 종류이며, 계층 모델입니다.
• 트리는 사이클이 존재 할 수 없습니다.
• 기본적으로 트리의 크기가 N 일 경우, 전체 간선의 갯수는 N-1개라고 볼 수 있다.
• 한개의 루트 노드만이 존재하며, 모든 자식 노드는 한 개의 부모 노드 만을 가진다.
• 트리 순회 (조회)의 방법은 전위 순회 (Pre-Order), 중위 순회 (In-Order), 후위 순회 (Post-Order)가 있습니다. 해당 순회 방법은 DFS/BFS 안에 해당된다.
• 트리의 종류에는 이진트리, 이진탐색트리, 균형트리, 이진힙 등이 있다.

순회의 종류

자 그럼 다시한번 위 그림을 기준으로 순회의 종류를 알아보자.

• 전위 순회 (Pre-Order) : 뿌리 노드를 먼저 방문 하는 순회 방법으로 (A -> B -> D -> G -> E -> C -> F) 순으로 순회 합니다.
• 중위 순회 (In-Order) : 왼쪽 하위 노드 트리를 방분 후 뿌리 노드를 방문 하는 순회 방법으로 (G -> D -> B -> E -> A -> F -> C) 순으로 순회 합니다.
• 후위 순회 (Post-Order) : 하위 노드 트리를 모두 방문 후 뿌리 노드를 방문 하는 순회 방법으로 (G -> D -> E -> B -> F -> C -> A) 순으로 순회 합니다.

트리의 종류

• 이진트리 (Binary Tree)

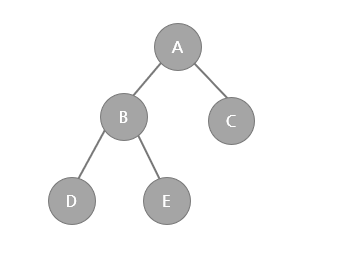
이진트리는 부모 노드가 최대 두개의 자식노드를 갖는 트리 구조를 말합니다. 다시 말해 자식노드는 하나일 수도 없을 수도 있습니다.

• 완전 이진트리 (Complete Binary Tree)

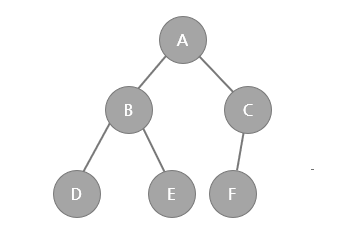
1. 완전 이진트리는 마지막 레벨을 제외하고 모든 노드가 채워져있는 트리구조를 말한다.
2. 마지막 높이의 노드 모두 채워져 있지 않아도 되지만, 노드가 왼쪽부터 채워져 있어야 한다. 만일 그림의 F가 왼쪽이 아니라 오른쪽이라면 해당 트리는 완전 이진트리가 아니다.

• 정 이진트리 (Full Binary Tree)

1. 정 이진트리는 모든 노드가 0개이거나 2개인 자식 노드만을 갖는 트리구조를 말한다.
2. 2 * 높이(height) => 노드의 갯수 n => 2^(높이(height)+1)-1

• 포화 이진트리 (Perfect Binary Tree)

1. 포화 이진트리는 모든 내부 노드가 두개의 자식 노드를 가지며 모든 노드가 동일한 깊이 또는 레벨을 갖는다.
2. 모든 말단 노드가 동일한 깊이를 가진다. 즉, 모든 노드가 0개 혹은 2개의 자식노드를 가진다.
3. 정 이진트리의 성질도 동일하게 만족한다.
4. 포화 이진 트리의 노드 개수는 2ⁿ⁻¹개 이다.

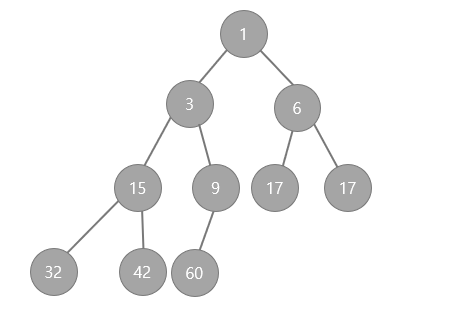
• 힙 (heap)

1. 여러 개의 값등 중에서 최댓값이나 최솟값을 빠르게 나타내도록 만들어진 자료구조이다.
2. 힙은 일종의 반정렬 상태(느슨한 정렬 상태) 를 유지한다.
   1. 큰 값이 상위레벨에 있고, 작은 값이 하위 레벨에 있다.
   2. 간단하게 말하자면 부모노드의 키 값이 자식노드의 키값보다 항상 큰 이진트리를 말한다.
3. 힙에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용 하지 않는다.)